本章节将逻辑回归,组织结构如下:
- Logistic Regression
- 6.1 Classification
- 6.2 Hypothesis Representation
- 6.3 Decision Boundary
- 6.4 Cost Function
- 6.5 Simplified Cost Function and Gradient Descent
- 6.6 Advanced Optimization
- 6.7 Multiclass Classification: One-vs-all
6.1 Classification
之前的回归是用来拟合数据 $(x,y)$ 的表达式,这里开始将分类问题,分类中,要预测的变量 $y$ 是离散值。比如给定一封邮件,看是否是垃圾邮件。我们将学习逻辑回归 (Logistic Regression) 算法。
在二分类中,我们将因变量分为两类,我们用 $y \in \{0,1\}$ 表示,其中0表示负类,1表示正类。这个的正负没有绝对含义。比如我们
在肿瘤检测中,判断是否恶性肿瘤,可以规定1表示恶性肿瘤,0表示良性肿瘤。
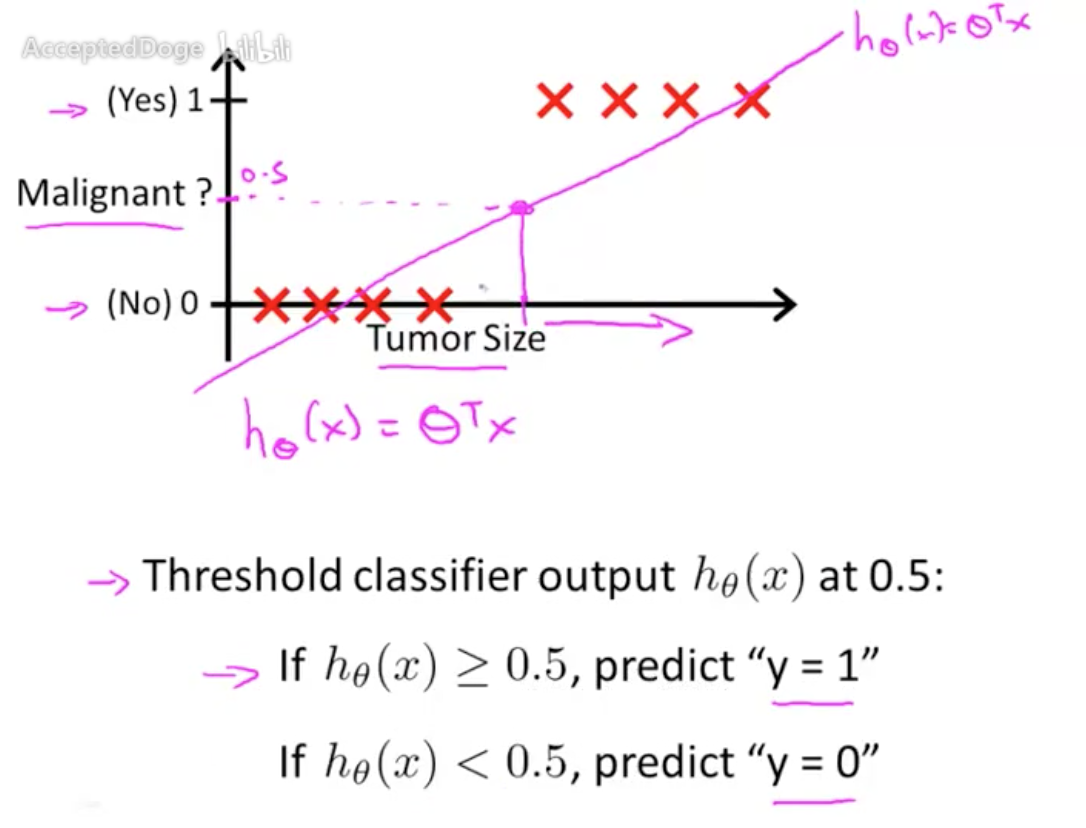
那么能否用线性回归的思路去解决二分类问题呢,比如我们拟合出 $h_{\theta}(x)$,然后以0.5位分界去判断分类结果。看上去可以实际上是会出问题的,比如以下这个数据,我们拟合到的是蓝色的直线,这个时候就会有很多点分类错误。

究其原因,是因为在分类当中,分类结果 $y$ 只能是 $y\in\{0,1\}$。
6.2 Hypothesis Representation
因此,我们引入一个新的模型,叫做逻辑斯特回归或逻辑回归,这个名字是有点 confusing 的,因为这是一个分类问题。我们想要的是 $0 \leq h_{\theta}(x) \leq 1$ 。线性回归的假设是 $h_\theta(x)=\theta^T x$,为了满足输出在 $[0,1]$中,我们将假设改为:
这个 $g(\cdot)$是什么呢,我们用的是大名鼎鼎的 sigmoid function(也叫 Logistic function),即:
这个函数是长这样的:

这个时候我们不妨思考 $h_{\theta}(x)$ 干了一件什么事呢,我们可以说,$h_{\theta}(x)$ 是对于给定的输入,输出变量等于1的可能性。即:
再联系上面的 S 型曲线,我们可以认为:
- 当 ${h_\theta}\left( x \right) \ge 0.5$ 时,预测 $y=1$;
- 当 ${h_\theta}\left( x \right)<0.5$ 时,预测 $y=$0。
如果我们不看 ${h_\theta}\left( x \right)$,而看 $z$,因为 $z=\theta^T x$ 也可以说:
- ${\theta^{T}}x \ge 0$,则 $y=1$
- ${\theta^{T}}x < 0$,则 $y=0$
6.3 Decision Boundary
假设有这样一个数据和逻辑回归模型:

我们假设学到的参数 $\theta = [-3,1,1]$,也就是说:$-3+x_1+x_2\ge0$时,预测为正类,即:

中间的这个用于分类的直线就叫做 decision boundary,翻译过来时判定边界,上述的例子是线性的判定边界,我们也可以扩充特征,得到非线性的判定边界,如远行的判定边界。

6.4 Cost Function
上面介绍了逻辑斯特回归的原理,那么我们怎么去拟合 $\theta$ 呢,即现在的问题为:

对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于将${h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}$带入到这样的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convexfunction)。
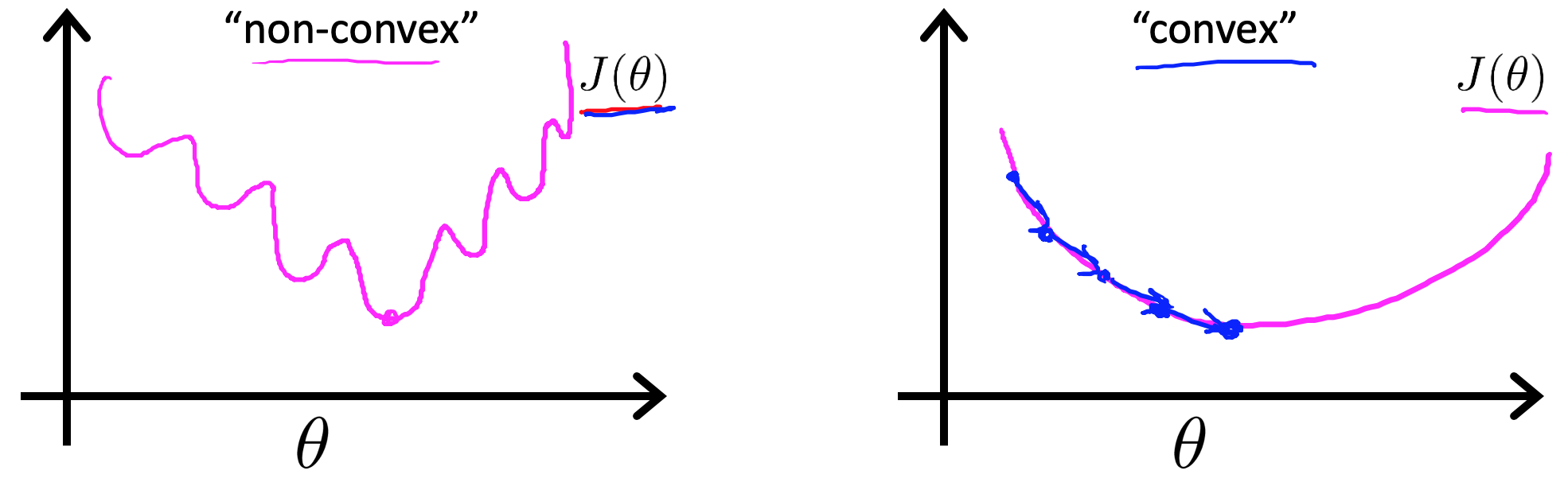
如果是非凸的,那么在迭代的过程中我们采用梯度下降法,就很难找到全局最小值了。联想线性回归的代价函数为:$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \frac{1}{2}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$,我们可以将代价函数写成这样的形式:$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$,在逻辑回归中,Cost为:

我们看一下这个 Cost 函数,如果是负类,那么判断正类的概率越大,cost 就越大,如果是正类,当贝判断为正类的概率越低,则 cost 越大。所以这个 cost 还是很符合直觉的。
6.5 Simplified Cost Function and Gradient Descent
那么当前的任务就可以表示为:
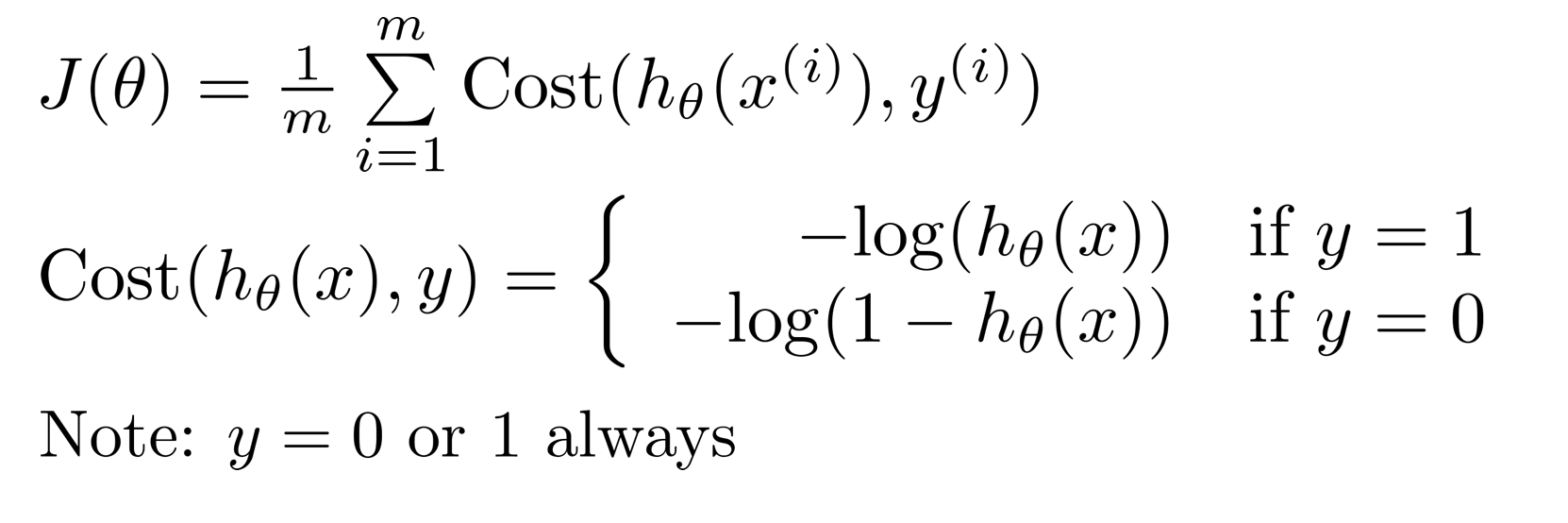
我们可以将上述的 Cost 做一个等价的变化,即:
带入到代价函数,即:
再结合假设函数,有:
再看一下求偏导:
虽然这个梯度下降推导的结果和线性回归看上去一样的,但是实际上是差别很大的。另外,这里也需要进行特征缩放。有了这个梯度的表达式,就可以很容易地去学习了。
6.6 Advanced Optimization
对于一个优化算法, 我们的目标是计算 Cost 的全局最优点。之前都是用的梯度下降法去寻找这个最优点,在数学上还有很多其他的方法:
- 共轭梯度法
- BFGS(变尺度法)
- L-BFGS(限制变尺度法)
如果以后接触,在考虑详细学习。
6.7 Multiclass Classification: One-vs-all
之前讨论的是用逻辑回归解决二分类问题,这里将多分类问题。这个问题在现实中是普遍存在的,比如天气预报,我们可以基本地分为晴天,阴天,雨天。这就是一个四分类问题了。
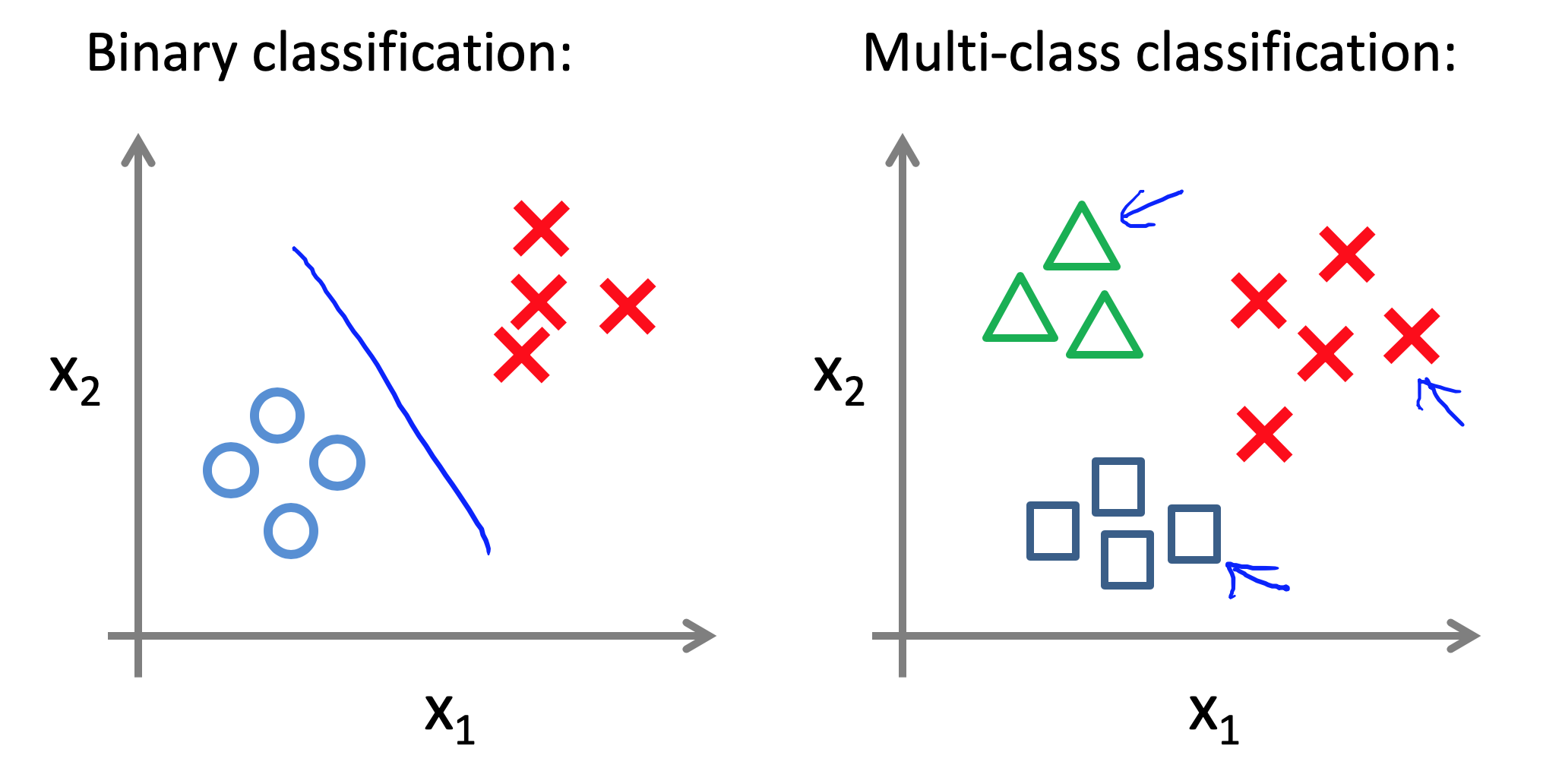
上图展示了一个二元分类和三元分类的例子。那么我们如何解决多元分类问题呢?我们把这个方法叫做 One-vs-all 方法。
我们可以将一个 $n$元分类问题转换为 $n$个二元分类问题,以晴天,阴天,雨天的天气分类来看,我们分为三个二元分类问题:
- 是不是晴天:将晴天对应的 $y$ 设为1,其他的天气设为0。
- 是不是阴天:…
- 是不是雨天:…

然后我们可以用逻辑回归得到是晴天的概率,是阴天的概率,是雨天的概率(不过这个概率和是不为1的)。然后我们选择概率最大的作为输出结果即可。这样我们就用逻辑回归完成了多元分类问题了。

